İki Nokta Arasındaki Uzaklık
Analitik geometride iki nokta arasındaki uzaklık soruları çok sık karşımıza çıkar. Bunun yanında analitik geometrinin her konusunda işlem yapmak için iki nokta arasındaki uzaklık formülü iyi bilinmelidir. Bu yazıda bunu detaylıca öğrenecek ve formülün de ötesine geçerek konuyu mantığıyla öğrenmeye çalışacağız.
İki doğru arasındaki uzaklığı, doğru denklemi yazmayı, noktanın noktaya göre ya da noktanın doğruya göre simetriğini alabilmek için bu konuyu iyi anlamanız gerekir.
İki Nokta Arasındaki Uzaklık Formülü
Sorularda bazen koordinat düzlemi üzerinden uzaklık bulmamız gerekebilir. Bazen de noktaları ifade edip de sizden hesaplama istenebilir. Bu formülün esası Pisagor bağıntısıdır. Aşağıdaki görselde iki nokta arasındaki uzaklık detaylı gösterilmiştir.
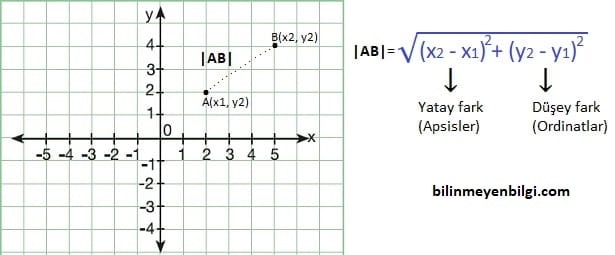
Pisagor bağıntısını aynen uyguluyoruz. İki noktanın arasındaki mesafe apsis değerleri (x’ler) ile ordinat değerlerinin (y’ler) karelerinin toplamının kare köküdür. Mantığını şekil üzerinden anladıktan sonra şekilli olmayan sorularda da çözüm sağlayabiliriz. Bununla ilgili aşağıdaki çözdüğümüz örneklere de bakabilirsiniz.
Bazı soru tiplerinde çizim yaparak geometri bilgisi kullanmanız gerekebilir. Bu nedenle formülü içselleştirmek için elinizden geldiği kadar şekli çizmeye çalışın. Daha sonraki süreçte koordinat düzlemi zaten kafanızda daha iyi canlanacaktır.
İki nokta arasındaki uzaklık formülü: IABI = √((x2 – x1)2 + (y2 – y1)2) şeklindedir.
İki Nokta Arasındaki Uzaklık Soruları
Biraz da soru çözerek öğrendiğimiz soruları pekiştirelim.
Soru #1: İki boyutlu koordinat düzlemi üzerinde K(0, 3) ve L(0, 9) şeklinde işaretlenen noktalar arasındaki mesafe kaç birimdir?
A) 2
B) 3
C) 4
D) 5
E) 6
Çözüm: Soruda her iki noktanın da apsis değerleri 0 olarak verilmiştir. Öyleyse ordinat değerleri doğrudan bize mesafeyi vermektedir. Apsis ve ordinat değerlerinden birinin aynı olduğu sorularda sayı doğrusunda iki nokta arasındaki uzaklık nasıl bulunuyorsa o şekilde hesaplama yaparız. Yani 9 – 3 = 6 bulunur. Doğru yanıt E seçeneğidir.
Soru #2: A(-1, 3) noktasıyla B(2, 7) noktaları birleştiriliyor. Bu şekilde elde edilen doğru parçasının uzunluğu |AB| kaç birimdir?
A) 1
B) 1,5
C) 4,7
D) 5
E) 6,2
Çözüm: Bu soru için formülü uygulamamız yeterli olacaktır. Önce apsisler farkı ve ordinatlar farkını bulalım. 2 – -1 = 3 ve 7 – 3 = 4 elde edilir. Şimdi bulduğumuz değerlerin karelerini toplayalım: 32 + 42 = 9 + 16 = 25 bulunur. Çıkan sonucun karekökünü alırsak |AB| = 5 birim bulunur. Cevap D seçeneğidir.
Soru #3: Analitik düzlemde A(1, 2) noktası alınıyor. Sonra A noktasını merkez kabul eden ve çapı 8 birim olan bir çember çiziliyor. Çember üzerindeki B noktasının koordinatları (k, 5) olduğuna göre k’nın pozitif değeri kaçtır?
A) 1
B) 3
C) 5
D) 7
E) 8
Çözüm: Çemberin çağı 10 birim olduğuna göre yarıçapı 5 birim olur. A noktası ile B noktasını birleştirdiğimizde yarıçapı elde ederiz. Öyleyse A noktası ile B noktası arasındaki mesafe 5 birim olacaktır. Formülü uyguladığımızda IABI = √((k – 1)2 + (5 – 2)2) = 5 bulunur.
Buradan da 5 = √((k – 1)2 + 9) ⇒ (k – 1)2 + 9) = 25 bulunur. Öyleyse (k – 1)2 = 16 elde edilir. Bu durumda k = 5 veya k = -3 olur. Pozitif değer dediği için cevap 5 olur. Doğru yanıt C seçeneğidir.
Diğer Bazı Formüller
Analitik geometride işimize yarayacak bazı diğer formülleri de kısaca paylaşalım.
Orta nokta formülü: A(a, b) ve B(c, d) noktalarının orta noktası C([a + b]/2, [c + d]/2) şeklindedir.
Nokta ile doğru arasındaki uzaklık: A(K, L) noktasının ax + by + c = 0 doğrusuna olan uzaklığı d = |a.k +b.L + c| / √a2+b2 formülü ile bulunur. Bulunan bu uzaklık noktanın doğruya olan dik uzaklığıdır. Bu da en kısa mesafe anlamına gelir.
İki doğru arasındaki uzaklık: İki doğru arasındaki uzaklıktan bahsedebilmemiz için bu iki doğrunun paralel olması gerekir. Çünkü paralel olmayan doğrular kesişir. Kesişen doğruların arasındaki uzaklıktan bahsetmek ise mümkün değildir. ax + by + c = 0 doğrusu ile ax + by + d = 0 paralel doğruları arasındaki uzaklık d= |c – d| / √a2+b2 şeklindedir.



